STEM Ptychography:
Basics & Applications
in the Physical Sciences

Prof. Dr. Philipp Pelz

FAU Erlangen-Nürnberg

Institute of Micro- and Nanostructure Research

Outline

Ptychography: The origins

Slides for this talk: https://tinyurl.com/MCptycho

• The diffraction signal in STEM contains the phase information of the sample

• Question: How can we measure the phase shifts of a sample in the electron microscope?

• Consider crystal:

If the lattice of diffraction peaks is convolved with an aperture larger than half the lattice spacing, interference reveals the relative phases

First ptychography setup by Walter Hoppe [1]

“The relative displacement of the origin must be performed to within fractions of 1 angstrom. There are two ways to do this: either the crystal can be moved relative to the illumination system, or the illuminating beam spot can be moved by changing the position of the beam source.” [3]

Walter Hoppe [1]

[1] Frank (2022, 2) Walter Hoppe (1983, 3) W. Hoppe (1969)

Ptychography and STEM

Hawkes 1982:

• “Ptychography was originally devised for the conventional transmission electron microscope, but has proved so difficult to put into practice [6] that interest in it, never intense, has dwindled almost to nothing, so far as I am aware.” [1]
• “since the space between the specimen and the detector plane(s) of a STEM is in principle freely accessible, is not this the ideal microscope for ptychography? Are STEM users unwitting ptychographers?” [1]

Diffraction pattern of a thin Si film by Nellist & Rodenburg 1995 [2]

Intensity in the overlap regions by Nellist & Rodenburg 1995 [2]

[1] Hawkes (1982, 2) Nellist, McCallum, and Rodenburg (1995)

Ptychography today: a flavour of 4D-STEM

Commercially available detectors provide diffraction patterns at >80kHz. Adapted from [1]

• The need to handle diffraction-space data streams and files is strong

• We will dicuss the current landscape of reconstruction algorithms and their approximations.

[1] Bekkevold et al. (2024)

Analytical Theory and Contrast Transfer

• The phase contrast transfer function (PCTF) describes how phase information is transferred in ptychography
• For weak phase objects, the PCTF can be written as:

\[ \text{PCTF}(\mathbf{Q}_p) = \frac{1}{2} \frac{\sum_{\mathbf{K}_f} |\Gamma_A(\mathbf{K}_f, \mathbf{Q}_p)|}{\sum_{\mathbf{K}_f} |A(\mathbf{K}_f)|} \]

where:

• \(\mathbf{Q}_p\) is the scanning spatial frequency
• \(\mathbf{K}_f\) are detector reciprocal space coordinates
• \(\Gamma_A = A^*(\mathbf{K}_f)A(\mathbf{K}_f - \mathbf{Q}_p) - A(\mathbf{K}_f)A^*(\mathbf{K}_f + \mathbf{Q}_p)\) is the aperture transfer function
• \(A\) is the aperture function

• The PCTF shows how different spatial frequencies are transferred
• Optimal transfer occurs when PCTF = 1
• Transfer is reduced when direct beam and diffracted beam do not interfere constructively

Note

The PCTF allows optimize defocus for best phase contrast for each sample

Analytical Theory and Contrast Transfer: Visual

Note

tune convergence angle and defocus to maximize phase contrast for your spatial frequencies of interest

Direct Reconstruction Methods

• Direct reconstruction methods aim to solve the phase problem without iterative optimization
• The Wigner Distribution Deconvolution (WDD) method:
  • Deconvolves the measured intensity from probe effects
  • Sensitive to noise and deconvolution hyperparameter
• The Single-Side Band (SSB) or Weak Phase Object (WPO) method:
  • deconvolution through multiplication in double Fourier space
  • SSB: fixed CTF independent on defocus
  • WPO: CTF dependent on defocus, high defocus beneficial

• Advantages:

  • Fast reconstruction without iterations
  • No hyperparameters to tune (SSB & WPO)
  • Computationally efficient

• Limitations:

  • May have artifacts from approximations
  • Works best for weak phase objects

Note

Direct methods provide rapid reconstruction (ms) and feedback

→ initial guess for iterative methods, live feedback

Weak Phase Object (WPO) Method

\[ \Psi(\mathbf{Q}_p) = \sum_{\mathbf{K}_f} \left\{ G(\mathbf{K}_f, \mathbf{Q}_p) \frac{\Gamma_A^*(\mathbf{K}_f, \mathbf{Q}_p)}{|\Gamma_A(\mathbf{K}_f, \mathbf{Q}_p)|} \right\}, \quad \text{for } \mathbf{K}_f \in |\{\Gamma_A(\mathbf{K}_f, \mathbf{Q}_p)| \neq 0\} \]

WPO ptychography setup and reconstruction workflow.
(d) Fourier transform gives complex 4D data in frequency domain.
(e) Frequency-dependent virtual detectors synthesized from phase plate.
(f) Phase correction of interference patterns.
(g) Object function calculated by integration over detector plane.
(h) Inverse Fourier transform yields reconstructed object function. [1]

Note

WPO contrast is strongly defocus dependent

[1] H. Yang et al. (2016)

Single-Side Band (SSB) Method

\[ \Psi(\mathbf{Q}_p) = \sum_{\mathbf{K}_f} \left\{ G(\mathbf{K}_f, \mathbf{Q}_p) \frac{\Gamma_A^*(\mathbf{K}_f, \mathbf{Q}_p)}{|\Gamma_A(\mathbf{K}_f, \mathbf{Q}_p)|} \right\}, \quad \text{for } \mathbf{K}_f \in \mathrm{double-overlap\,region} \]

Phase (top) and amplitude (bottom) of \(G(\mathbf{K}_f, \mathbf{Q}_p)\) as a function of \(\mathbf{K}_f\) for three \(\mathbf{Q}_p\) values with significant amplitude extracted from a four dimensional dataset from a sample of graphene.[1]

Note

SSB contrast is independent of defocus

[1] Pennycook et al. (2015)

Bayesian Framework for Inverse Problems

• Goal: Estimate unknown image \(\mathbf{x}\) from a diffraction pattern amplitude \(\mathbf{y}\)
• \(p(\mathbf{x} | \mathbf{y})\): posterior probability of the unknown image given the diffraction pattern
• The most likely image, given the measurements:

\[\boxed{\hat{\mathbf{x}} = \arg\min_{\mathbf{x}} -\log p(\mathbf{y}|\mathbf{x}) - \log p(\mathbf{x})}\]

\[\begin{align*} \hat{\mathbf{x}} &= \arg\max_{\mathbf{x}} p(\mathbf{x}|\mathbf{y}) \\ &\overset{(i)}{=} \arg\max_{\mathbf{x}} \frac{p(\mathbf{y}|\mathbf{x})p(\mathbf{x})}{p(\mathbf{y})} \\ &\overset{(ii)}{=} \arg\max_{\mathbf{x}} p(\mathbf{y}|\mathbf{x})p(\mathbf{x}) \\ &\overset{(iii)}{=} \arg\max_{\mathbf{x}} \log\left(p(\mathbf{y}|\mathbf{x})p(\mathbf{x})\right) \\ &= \arg\min_{\mathbf{x}} -\log p(\mathbf{y}|\mathbf{x}) - \log p(\mathbf{x}). \end{align*}\]

• 1. Bayes’ rule: \(p(\mathbf{x} | \mathbf{y}) = \dfrac{p(\mathbf{y} | \mathbf{x})\, p(\mathbf{x})}{p(\mathbf{y})}\)
     
• 2. \(p(\mathbf{y})\) does not depend on \(\mathbf{x}\)
     
• 3. The log-likelihood increases monotonically

Note

Many modern ptychography algorithms use a Bayesian framework

Bayesian Framework for Ptychography

The likelihood for a linear forward model with Gaussian noise is:

\[ p(\mathbf{y}|\mathbf{x}) \sim \exp\left(-\frac{1}{2\sigma^2} \|\mathbf{P}(\mathbf{x}) - \mathbf{y}\|_2^2\right) \]

where \(\mathbf{P}\) is the ptychography measurement operator, \(\mathbf{x}\) is the unknown image, \(\mathbf{y}\) is the measured data, and \(\sigma^2\) is the noise variance. The negative log-likelihood for a forward model with Gaussian noise is:

\[ -\log p(\mathbf{y}|\mathbf{x}) = \frac{1}{2\sigma^2} \|\mathbf{P}(\mathbf{x}) - \mathbf{y}\|_2^2 + c \] The prior term \(-\log p(\mathbf{x})\) is often called the regularization in optimization. It can be written as: \[ \lambda \sigma^2 \mathcal{R}(\mathbf{x}) = -\log p(\mathbf{x}) \] where \(\mathcal{R}(\mathbf{x})\) is a regularization function (e.g., enforcing smoothness or sparsity), \(\lambda\) is a regularization parameter, and \(\sigma^2\) is the noise variance. The resulting optimization problem for MAP estimation in the case of a linear forward model and Gaussian noise is:

\[ \hat{\mathbf{x}} = \arg\min_{\mathbf{x}} \frac{1}{2} \|\mathbf{P}(\mathbf{x}) - \mathbf{y}\|_2^2 + \lambda \mathcal{R}(\mathbf{x}) \]

where

• \(\mathbf{P}(\mathbf{x})\) is the measurement operator,

• \(\mathbf{y}\) is the measured data,

• \(\mathcal{R}(\mathbf{x})\) is the regularization (prior) term, and

• \(\lambda\) controls the strength of the regularization.
  
  

• first term enforces data fidelity

• second term encodes prior knowledge or constraints on the solution (regularization)

Iterative Reconstruction Methods: Basic Ptychography Algorithm

import torch
import torch.fft as fft
from torch import Tensor
import skimage.data as skdata  
import skimage.transform as sktrans
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter
import numpy as np
img = skdata.astronaut()

img = sktrans.resize(img, (64, 64))
img = gaussian_filter(img, sigma=1)
# Convert to grayscale by taking mean across color channels
img = np.mean(img, axis=2)
img = img.astype(np.float32) / 255.0
img = torch.from_numpy(img)  
complex_image = torch.polar(torch.ones_like(img), img/img.max()*0.4)

Ingredient 1: scanning over the sample

def C(image : Tensor, positions : Tensor, window_size : int) -> Tensor:
    # Cropping operator: crop windows from the image at the given positions
    scan_windows = [] 
    for i, (x, y) in enumerate(positions):
        x_indices = torch.arange(x, x + window_size) % image.shape[1]
        y_indices = torch.arange(y, y + window_size) % image.shape[0] 
        Y, X = torch.meshgrid(y_indices, x_indices, indexing='ij') 
        window = image[Y, X]
        scan_windows.append(window)        
    scan_windows = torch.stack(scan_windows, dim=0)
    return scan_windows

Ingredient 2: propagation / interference

def F(wave):
  return fft.fft2(wave)

Simplest Ptychography Model

\[P(\mathbf{x}, \mathbf{\psi}, \mathbf{\rho}) = \left| \mathcal{F} \left( \mathbf{\psi(r)} \cdot \mathbf{C}(\mathbf{x}, \mathbf{\rho}) \right) \right|\]

def P(sample, probe, scan_positions):
  # crop the scanning windows, transmit the beam, propagate 
  # to detector, then detect
  return th.abs(F(probe * C(sample, scan_positions, probe.shape[0])))

import numpy as np
import plotly.graph_objects as go
import plotly.io as pio

# Configure plotly for both VS Code and Quarto rendering
pio.renderers.default = "plotly_mimetype+notebook_connected"

# Define scan grid
size = 8
step = 1
x = torch.arange(0, size, step)
y = torch.arange(0, size, step)
X, Y = torch.meshgrid(x, y, indexing='ij')
positions = torch.stack([X.flatten(), Y.flatten()], dim=1)  # Kx2 array
K = positions.shape[0]

# Example sample image (replace with your own)
sample = complex_image

# Example probe (window size)
probe_size = 32 
probe = torch.ones((probe_size, probe_size))

# Crop image stack
image_stack = C(sample, positions, probe_size)  # shape: (K, probe_size, probe_size)

# Create interactive plotly figure with title "scanning windows"
fig = go.Figure()
# Add initial image
fig.add_trace(go.Heatmap(
    z=np.angle(image_stack[0].detach().cpu().numpy()),
    colorscale='inferno',
    showscale=False
))
# Add slider, set black background, add figure title, and set text color to white
fig.update_layout(
    title=dict(text="Scanning Windows", font=dict(color='white')),
    width=400,
    height=500,
    margin=dict(l=0, r=0, t=40, b=0),
    xaxis=dict(showticklabels=False, showgrid=False, color='white', title_font=dict(color='white')),
    yaxis=dict(showticklabels=False, showgrid=False, color='white', title_font=dict(color='white')),
    sliders=[dict(
        active=0,
        currentvalue={"prefix": "Position: ", "font": {"color": "white"}},
        len=0.9,
        x=0.1,
        xanchor="left",
        y=0,
        yanchor="top",
        steps=[dict(
            method="restyle",
            args=[{"z": [np.angle(image_stack[i].detach().cpu().numpy())]}, [0]],
            label=str(i)
        ) for i in range(K)],
        font=dict(color='white')
    )],
    paper_bgcolor='black',
    plot_bgcolor='black',
    font=dict(color='white')
)
fig.show()

Experimental Design Considerations: parameter flexibility

Adjustable parameters for ptychographic data acquisition [1]

Limitation/check	Description	Default
Areal oversampling	How many probes illuminate each pixel? \[A = \frac{\pi r_p^2}{s^2}\]	1.6 - 1e3
Probe sampling	To which extent is the probe contained in its window? \[P = \frac{1}{2r_pd}\]	< 0.5
Ronchigram magnification	Size of the shadow image on the detector plane in units \(\frac{pixel}{Å}\) \[M = \frac{\alpha}{\theta \cdot r_p} = \frac{\alpha}{\lambda d \cdot r_p}\]	10 - 100

where:

• \(\alpha\) is the semi-convergence angle
• \(\theta\) is the angular sampling in radians
• \(s\) is the scan step size

• \(r_p\) is the probe radius
• \(d\) is the diffraction space sampling

[1] Skoupy et al. (2025, 2) Gilgenbach, Chen, and LeBeau (2024)

Experimental Design Considerations: sampling

Note

sampling in diffraction space & defocus → Ronchigram Magnification

sampling in real space & defocus → Areal oversampling

Modeling partial coherence

• partial coherence arises from multiple sources in electron microscopy:
  • finite source size –> partial spatial coherence of the electron source [1]
  • finite detector pixel size –> partial spatial coherence
  • finite energy spread inside the column –> partial temporal coherence [1]

• most efficient models:
  • detector pixel size & source size: convolution in the detector plane [2]
  • energy spread & remaining partial coherence: multiple coherent modes [3]

\[ I(\vec{\rho}, \vec{q}) =\left(\color{red}{\sum_n a_n} \left|\mathcal{F}\left[O(\vec{\vec{r}})\color{red}{\psi_n(\vec{r}-\vec{\rho})}\right]\right|^2\right) \color{green}{\otimes M(\vec{q})} \]

where:

• \(\vec{\rho}\) is the position on the detector plane
• \(\vec{q}\) is the position in reciprocal space
• \(a_n\) is the amplitude of the \(n\)-th coherent mode

• \(O(\vec{r})\) is the aperture function
• \(\psi_n(\vec{r}-\vec{\rho})\) is the wave function of the \(n\)-th coherent mode, shifted by the position \(\vec{\rho}\)
• \(M(\vec{q})\) is the a function modeling modulation transfer function and partial source coherence

[1] Z. Li et al. (2022), [2] Diederichs et al. (2024), [3] Thibault and Menzel (2013)

Experimental Design Considerations: coherence

Note

temporal coherence is no problem at 200-300kV, ~2-3 modes

at low energies 30-60keV, temporal coherence needs more modes

superresolution capabilities circumvent the coherence problem

Adding more “nuisance parameters”: Refining the scan positions

• realistic model for thin samples:

\[ P(\mathbf{x}, \mathbf{\psi}, \mathbf{\rho}) = \left|\left(\sum_n a_n \left|\mathcal{F}\left[O(\vec{\vec{r}})\psi_n(\vec{r}-\vec{\rho})\right]\right|^2\right) \otimes M(\vec{q})\right| \]

\[ \hat{\mathbf{x}} = \arg\min_{\color{red}{\mathbf{x}, \mathbf{\psi}, \mathbf{\rho}}} \frac{1}{2} \|P(\mathbf{x}, \mathbf{\psi}, \mathbf{\rho}) - \mathbf{y}\|_2^2 + \lambda \mathcal{R}(\mathbf{x}) + \lambda_1 \mathcal{R}_1(\mathbf{\psi}) \]

Note

modern ML frameworks allow us to refine additional parameters easily using automatic gradient calculations

Modeling thick samples: the multi-slice algorithm

• Up to now: thin samples, i.e. thickness < depth of field and weak scattering

• Thick samples require modeling of multiple scattering events
• Sample is divided into thin slices that can be treated independently
• Beam propagates through slices sequentially

Multi-slice propagation model (Adapted from [1])

\[\psi_{n+1}(r) = \mathcal{P}_{\Delta z} \left[ t_n(r) \psi_n(r) \right]\]

where:

• \(\psi_n(r)\) is the wave at slice n
• \(t_n(r)\) is the transmission function
• \(\mathcal{P}_{\Delta z}\) is the propagator (usually Fresnel)
• \(\Delta z\) is the slice thickness

Key parameters:

• Slice thickness (typically 1-2 nm)
• Number of slices
• Propagation distance

[1] Romanov et al. (2024), [2] First demonstration: Chen et al. (2021)

Multi-slice ptychography (MSP)

Component	Mathematical Description
Multislice algorithm	\[\mathcal{M}_{\psi}(\mathbf{V}) = \prod_{k=0}^T (\mathcal{P}^{\Delta z} T^{\mathbf{V}_k})\psi \]
Multi-slice ptychography model	\[P(\mathbf{V}, \mathbf{\psi}, \mathbf{\rho}) = \left|\left(\color{red}{\sum_n a_n} \left|\mathcal{F}\left[\mathcal{M}_{\color{red}{\psi_n(\vec{r}-\vec{\rho})}}(\mathbf{V})\right]\right|^2\right) \color{green}{\otimes M(\vec{q})}\right|\]
Optimization problem	\[\hat{\mathbf{V}} = \arg\min_{\mathbf{V}, \mathbf{\psi}, \mathbf{\rho}} \frac{1}{2} \|P(\mathbf{V}, \mathbf{\psi}, \mathbf{\rho}) - \mathbf{y}\|_2^2 + \lambda \mathcal{R}(\mathbf{V}) + \lambda_1 \mathcal{R}_1(\mathbf{\psi}) \]

Note

We have arrived at the state of the art in ptychography:

3D imaging with deep-sub-angstrom lateral and ~2nm depth resolution

Constraints in MSP: positive potential, amplitude~1, blur kernel

Constraint 1: Positive Potential

• The electrostatic potential \(V(\mathbf{r})\) must be physically meaningful: \(V(\mathbf{r}) \geq 0\)
• Enforced during optimization by projecting negative values to zero
• Prevents unphysical solutions and improves stability

Constraint 2: Amplitude \(\approx 1\)

• The transmission function \(t_n(\mathbf{r})\) should have amplitude close to 1 (very few electrons scattered outside the 4D-STEM detector are registered as “amplitude contrast”)
• Enforced by regularization: penalize deviations from \(|t_n(\mathbf{r})| = 1\)

Constraint 3: Blur Kernel

• in (x,y) plane: stabilize deep-sub-angstrom resolution reconstructions
• in z-direction: limit depth resolution, disallow higher than 1nm depth resolution
• early algorithms: Fourier-space convolution –> leads to wrap-around artefacts for non-periodic samples

Note

Minimal set of constraints to make the reconstruction stable.

Add your own flavour of constraints: more physics, data-driven priors, denoisers…

Extensions of MSP: mistilt correction

Slight misorientation of the zone axis can lead to stricter requirements for the slice thickness.
Solution: include the mistilt in the propagator, refine it during the reconstruction
Adapted from [1]

Adaptive propagator requires less slices
–> Faster reconstructions
Adapted from [1]

Note

Slight deviations from the perfect zone axis can be refined algorithmically

[1] Sha, Cui, and Yu (2022)

Extensions of MSP: atomistic models

Assemble the electrostatic potential from atomic positions and atomic numbers

\[O_l(\mathbf{r}) = A_l(\mathbf{r}) e^{i \sigma_e V_{\mathrm{FP}}^{(j)}(\mathbf{r}, \boldsymbol{\tau})}\]

\[ V_{\mathrm{FP}}^{(j)}(\mathbf{r}, \boldsymbol{\tau}) = \sum_{n=1}^{N} w_n v_{Z_n} \left( \mathbf{r} - \mathbf{r}_n - \sqrt{\langle u_n^2 \rangle} \cdot \mathbf{g}_{n, \tau} \right) \]

Atomistic model for the reconstructed potential (Adapted from [2])

Note

Atomic positions can be refined directly

–> interpretable model, enables phonon modeling

–> sparse model –> achieves higher resolution than voxelized models

–> phonon modeling –> might enable imaging of phonon modes

[1] W. Yang et al. (2024, 2) Diederichs et al. (2024)

Applications of MSP: 3D imaging

Adapted from [1]: Identification of O vacancies in ZSM-5. Intensity histograms and variations reveal O vacancies through comparison of experimental and simulated ptychographic phase images. Red dots in (D) show identified vacancy-containing columns across layers L1-L7.

Adapted from [1]: (A) 4D-STEM ptychography image displaying extra T atoms (indicated by the magenta arrows) relative to the typical MFI framework. The yellow dashed rectangle indicates the region analyzed in Fig. 5A. (B) Structural projections of straight 10-MR channels of MFI and MEL and their superposition. The letters i and m denote inversion and mirror symmetry, respectively. (C and D) Second (C) and fourth (D) slices of the multislice ptychography reconstruction result.

Note

Excellent for imaging inhomogeneities of weakly scattering atoms

[1] Zhang et al. (2023)

Applications of MSP: 3D imaging 2

Adapted from [1]: Hydrogen detection sensitivity across different imaging techniques. (A) Simulated images of NbHx (15 nm thickness) with varying hydrogen content over Nb metal atoms (0.36-2.0 H/M) acquired by contrast-inverted annular bright-field (ABF), integrated center-of-mass (iCOM), and multislice electron ptychography (MEP). Scale bar, 2 Å. (B) Hydrogen-to-metal column intensities vs hydrogen content for iCOM and MEP, demonstrating MEP’s superior detection sensitivity.

Adapted from [1]: TiH2 phase images along [100] and [110] zone axes using experimental data, summing middle slices (11-22 nm thickness)

Note

Even hydrogen columns can be resolved, if more than 4 H atoms.

[1] P. Li et al. (2025)

Applications of MSP: ultra low-dose imaging

Adapted from [1]: MOF Zr-BTB imaged with electron ptychography at 115 e−/Å2 dose. (a) Phase image showing 2.25 Å resolution. (b-d) Power spectrum, enlarged region, and structural model showing excellent agreement.

Adapted from [1]: Iterative reconstruction error curves (d) and reconstructed ptychography phase images (e) using 4D-STEM datasets simulated at varying convergence semiangles with a consistent electron dose of 100 e−/Å2. The 10-mrad case shows the best reconstruction, as marked by the red square.

Note

Multiple scattering from crystals at very low doses enables 2Šresolution at dosesof 100 e-/Ų

[1] G. Li et al. (2025)

Limitations of MSP: axial resolution

Adapted from [1]: Principle of depth sectioning via multislice electron ptychography

Adapted from [1]: Depth evolution of phase/intensity across Pr-Pr dumbbell showing strong dependence on chromatic aberration. Comparison between (a) multislice ptychography and (b) focal series ADF imaging.

Note

Axial resolution of MSP is (with current algorithms) limited to below atomic scale if not using the most cutting edge instrumentation

[1] Chen et al. (2024)

Calibrations

• Need to know with good accuracy:

  • reciprocal space sampling
  • real space sampling
  • convergence angle
  • detector rotation

• measuring diffraction sampling and alpha

• PACBED from known crystal

• measuring real space sampling: image known crystal in real space

• FFT and measure bragg spacing

• measure line profile

• rotation: curl of DPC signal != 0, minimize curl

First unknown 3D atomic structure solved with 4D-STEM tomography

Approach:

1. 4D-STEM tilt series
2. mixed-state ptychography of all tilt angles

3. Joint linear tomography and alignment
4. Sub-pixel atomic peak tracing
5. 3D atomic structure determination

Volume size: (6 nm)³

Note

Elliptic double-wall CNT and complex inner structure resolved in 3D

Pelz et al. (2023)

Full 3D: Single-Slice Ptychographic Tomography Solves Nanostructures

Note

First 3D atomic structure solved with phase-contrast tomography.
Novel ZrTe₂ phase, confirmed stable with DFT simulations.

Pelz et al. (2023)

Depth Resolution Progress Over Time

2022: 2.2 Å in 6nm thick volume using SSPT [1]

2023: 2.0 Å in 18nm thick volume using MSPT [2]

2024: 0.8 Å in 11nm thick volume using E2E-MSPT [3]

Note

Algorithm development drives resolution records and depth of focus enhancements

Pelz et al. (2023), Romanov et al. (2024), You, Romanov, and Pelz (2024)

Full 3D: multis-slice ptychographic tomography

Perform MSP reconstruction
for each tilt angle
and project the potential along z







✅ Advantages:
- Decouple tomographic alignment from ptychographic reconstruction
- Can use positions and alignment as input to E2E-MSPT

Multi-slice Ptychographic Tomography forward model

❌ Disadvantage:
- Loses some 3D info from MSP

Romanov et al. (2024)

Joint Tomography and Rigid Alignment enables atomic resolution of beyond-DOF volumes

Note

Enabled by reaching sub-pixel alignment at each scale

Romanov et al. (2024)

3x DOF volumes display atomic resolution

Note

Volume size: (18.2 nm)³ Voxel size: 0.3 Å

Romanov et al. (2024)

Orthoslices reveal lattice in all 3 dimensions

scale: 1 nm

Note

Lattice resolved, but Co atom contrast overpower O contrast
=> Around 1 Å z resolution required to resolve O atoms

Romanov et al. (2024)

End-to-end reconstruction - putting all pieces together

Fully E2E-MSPT reconstruction includes

1. affine resampling of potential volume
   
2. z-resampling of potential volume (save compute)
   
3. batch-croppping and mixed-state multi-slice model
   
4. far-field propagation
   
5. gradient backpropagation through full model

Note

The most accurate approximation for 4D-STEM tomography to-date

You, Romanov, and Pelz (2024)

Outlook 1: From Imaging Structure to Imaging Fields

Some open topics:

1. can we image and directly measure valence electron distributions?

Adapted from [1]: Detecting charge transfer in WS2. SSB phase images show electron transfer from W to S atoms, with experimental results matching DFT predictions. Charge density differences between IAM and DFT models reveal valence electron distributions.

2. can we image and directly measure atomic-scale magnetic fields?

Adapted from [2]: Joint electron ptychography reconstruction of NiO showing electrostatic and magnetic potentials in 2D and 3D

[1] Hofer et al. (2025), [2] Yalisove, Varnavides, and Scott (2025)

Some open topics:

3. can we image and directly measure phonon modes without a spectrometer?

Adapted from [3]: Principles of numerical diffraction pattern formation in ptychography. Schematic showing multislice simulation, incoherent scattering effects from finite source size and thermal motion, and reconstruction models of increasing complexity from 2D to 4D mixed-object ptychography.

Adapted from [3]: Ptychographic reconstructions showing atomic vibrations in silicon. Ground truth from MD simulation (a) compared to reconstructions with different coherence models (b-e). Multiple probe modes enable accurate recovery of correlated atomic motion.

Note

We will see continued improvements in quantitative imaging of physical quantities accessible by electron microscopy

[1] Hofer et al. (2025), [2] Yalisove, Varnavides, and Scott (2025), [3] Gladyshev et al. (2023)

Outlook 2: From Imaging Static Structure to Imaging Dynamics

Open topics:

• algorithms fast enough for real-time imaging ➜ in-situ ptychography

Adapted from [1]

• 3D depth sectioning methods fast enough for in-situ studies

Adapted from [2]: 3D cuboid representation of a GAA-transistor reconstruction, illustrating all sliced planes withlabeled components visible in three dimensions. The cuboid dimensions are 18 nm × 13 nm ×33 nm (not to scale in depth)

Note

We will see in-situ applications of ptychography as the codes become faster and more standardized

[1] Crozier et al. (2025), [2] Karapetyan et al. (2025)

Outlook 3: From Imaging Ordered Structures to Imaging Disorder

• can we image weakly scattering amorphous materials in 3D?

Adapted from [2]

requires high axial resolution, highly challenging for tomography

• can we image 3D structure of polymers or biomaterials?

Adapted from [1]

Note

We will see images and volumes of more and more disordered structures

[1] Pei et al. (2023), [2] Karapetyan et al. (2025)

Summary

• Ptychography has a multitude of experimental settings to control and algorithms to explore
• When tuned well, results well beyond hardware capabilities can be expected
• Modern ML tools alleviate algorithm development and application by non-experts

Open positions at FAU

• 13 open Ph.D. positions in the new Graduate School “Correlative Microscopy”
• Develop Sensor Fusion of 4D-STEM + APT, 4D-STEM + EELS, 4D-STEM + Raman Microscopy

References 📚

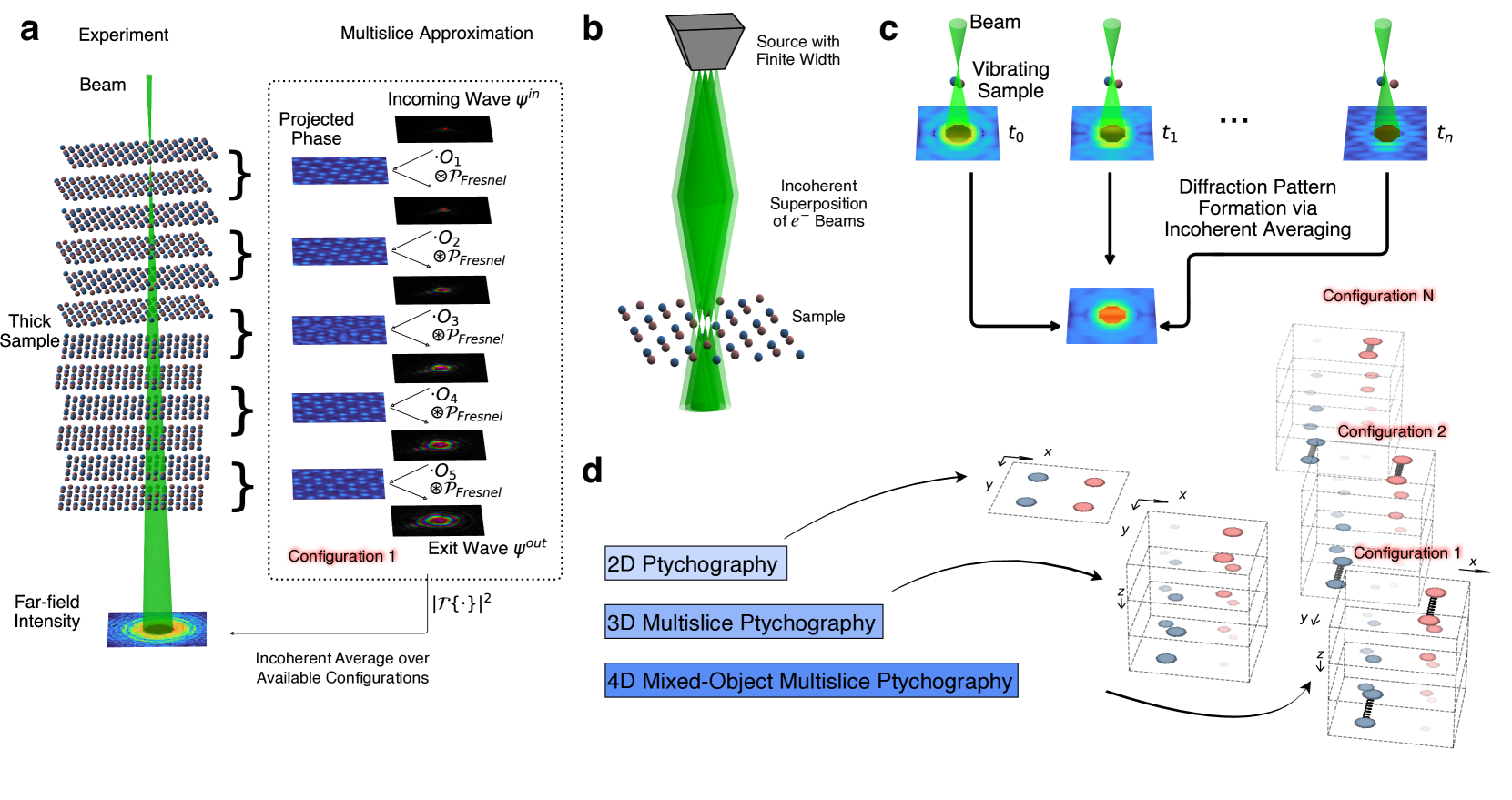
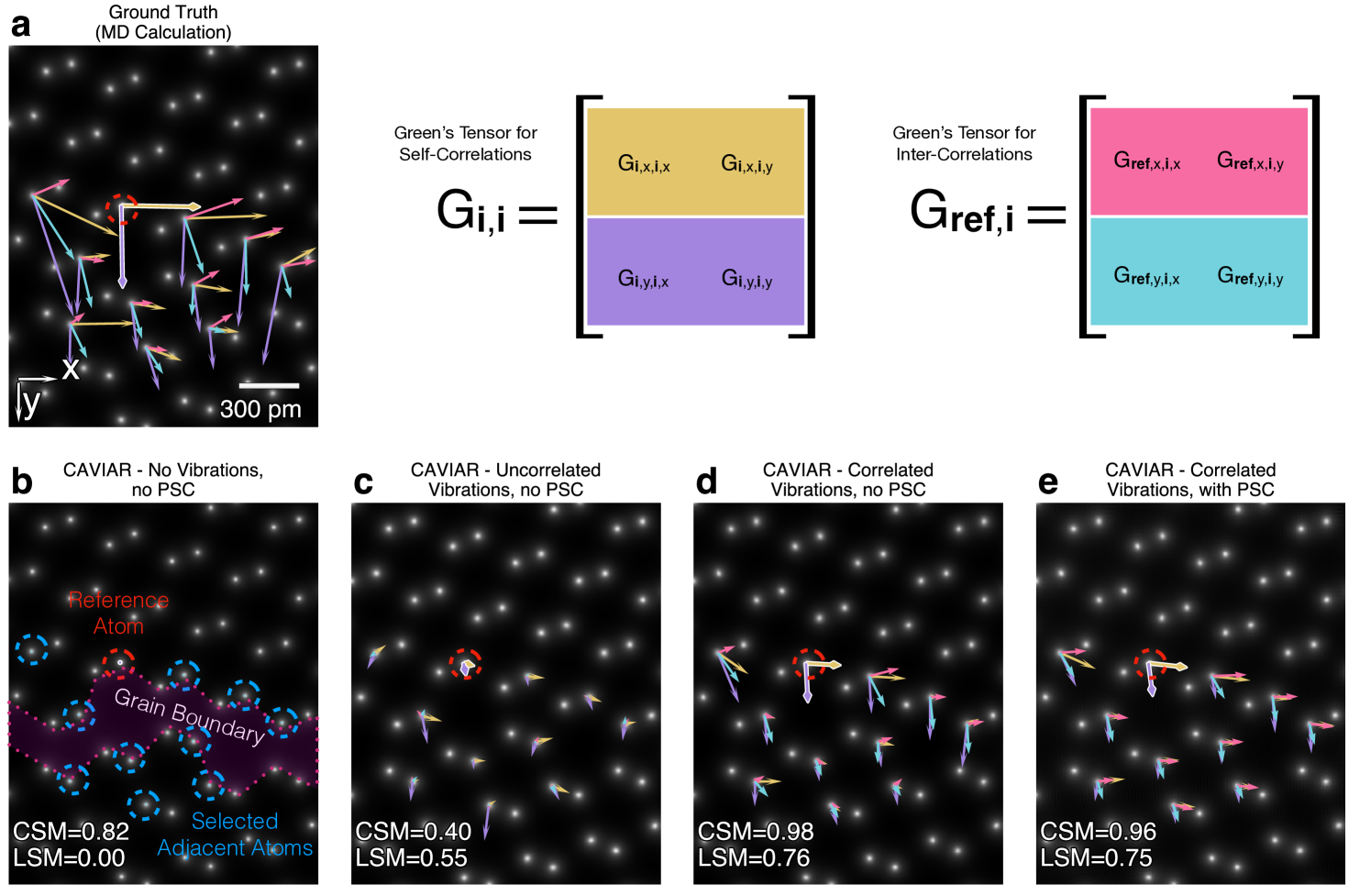
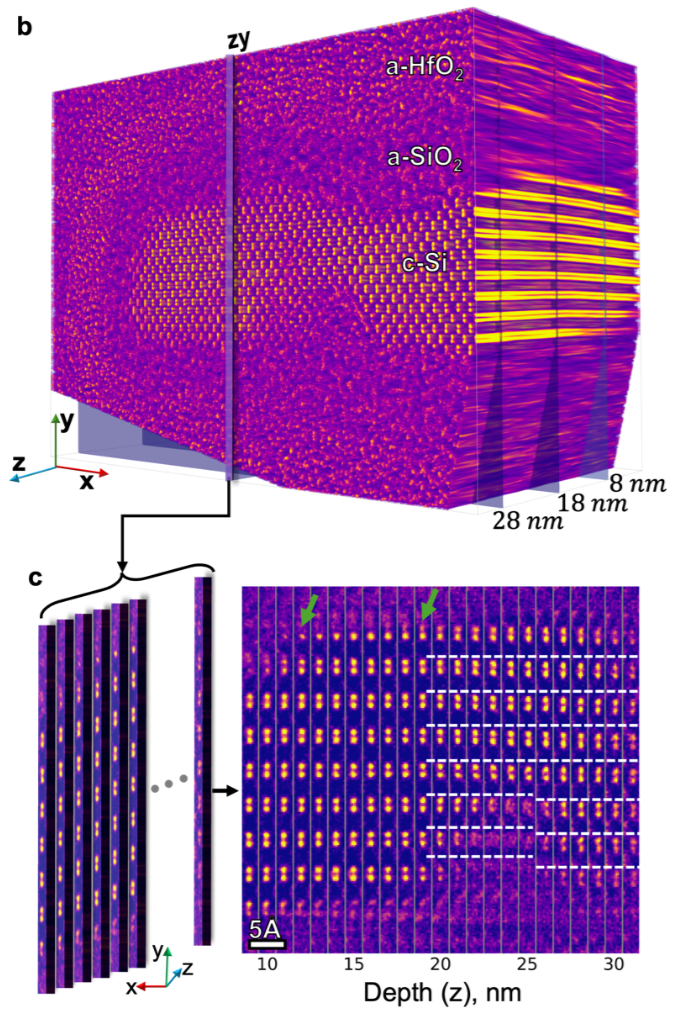
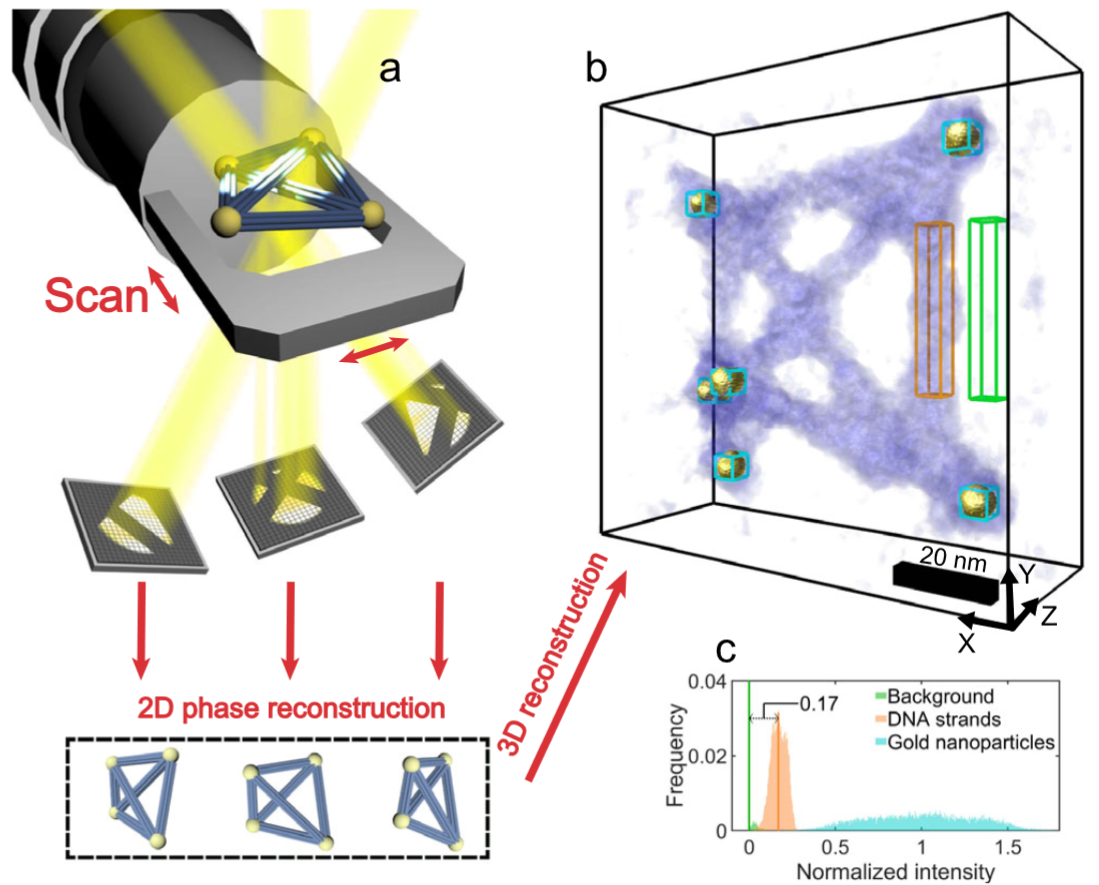
Bekkevold, Julie Marie, Jonathan J P Peters, Ryo Ishikawa, Naoya Shibata, and Lewys Jones. 2024. “Ultra-Fast Digital DPC Yielding High Spatio-Temporal Resolution for Low-Dose Phase Characterization.” Microscopy and Microanalysis 30 (5): 878–88. https://doi.org/10.1093/mam/ozae082.

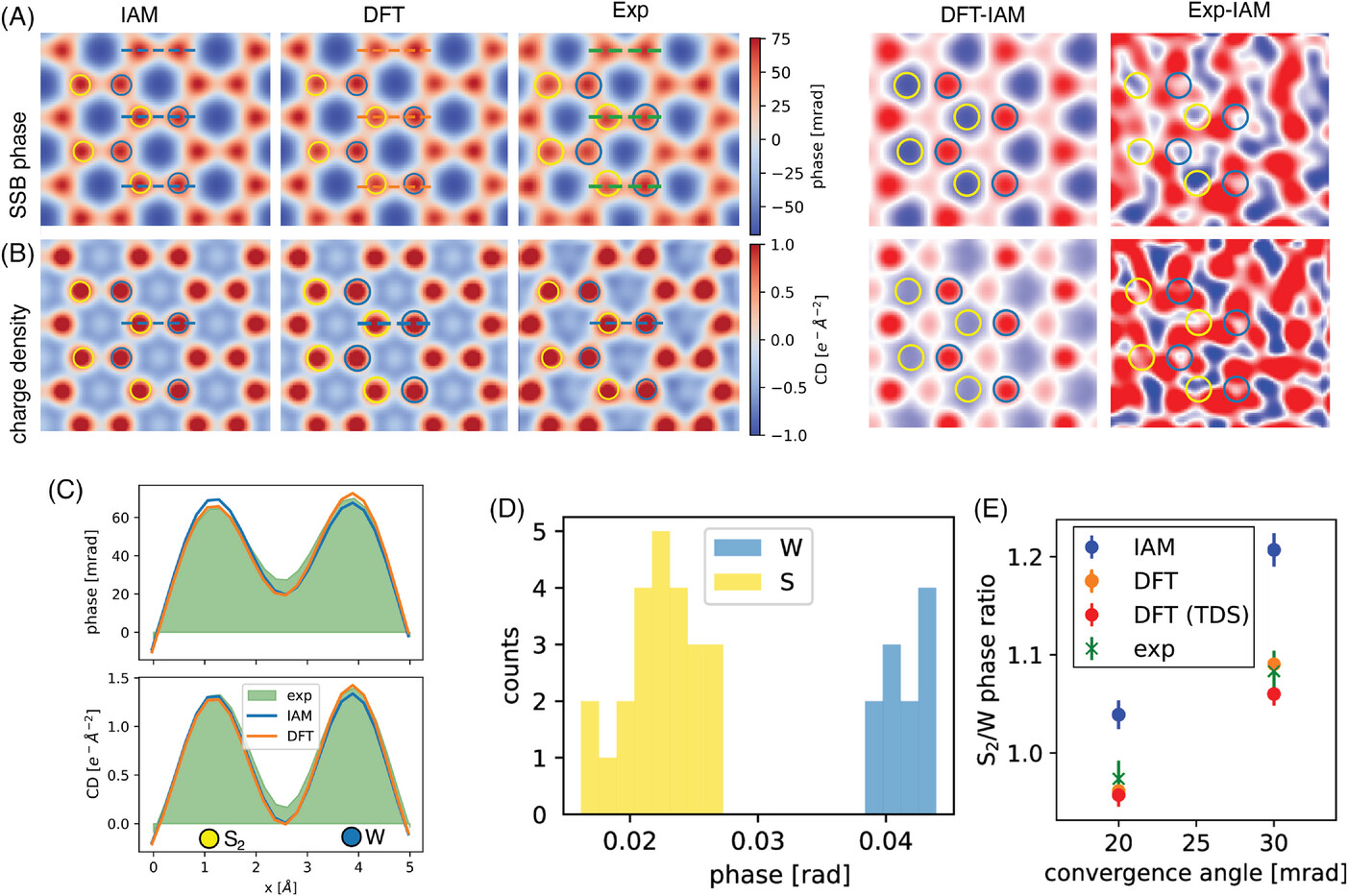
Chen, Zhen, Yi Jiang, Yu-Tsun Shao, Megan E. Holtz, Michal Odstrčil, Manuel Guizar-Sicairos, Isabelle Hanke, Steffen Ganschow, Darrell G. Schlom, and David A. Muller. 2021. “Electron Ptychography Achieves Atomic-Resolution Limits Set by Lattice Vibrations.” Science 372 (6544): 826–31. https://doi.org/10/gkb46j.

Chen, Zhen, Yu-Tsun Shao, Steven E. Zeltmann, Harikrishnan K. P, Ethan R. Rosenberg, Caroline A. Ross, Yi Jiang, and David A. Muller. 2024. “Imaging Interstitial Atoms with Multislice Electron Ptychography,” no. arXiv:2407.18063 (July). https://doi.org/10.48550/arXiv.2407.18063.

Crozier, Peter A., Matan Leibovich, Piyush Haluai, Mai Tan, Andrew M. Thomas, Joshua Vincent, Sreyas Mohan, et al. 2025. “Visualizing Nanoparticle Surface Dynamics and Instabilities Enabled by Deep Denoising.” Science 387 (6737): 949–54. https://doi.org/10.1126/science.ads2688.

Diederichs, Benedikt, Ziria Herdegen, Achim Strauch, Frank Filbir, and Knut Müller-Caspary. 2024. “Exact Inversion of Partially Coherent Dynamical Electron Scattering for Picometric Structure Retrieval.” Nature Communications 15 (11): 101. https://doi.org/10.1038/s41467-023-44268-x.

Frank, Joachim. 2022. “Chapter Three - Walter Hoppe — x-Ray Crystallographer and Visionary Pioneer in Electron Microscopy.” In Advances in Imaging and Electron Physics, edited by Peter W. Hawkes and Martin Hÿtch, 221:45–69. The Beginnings of Electron Microscopy - Part 2. Elsevier. https://doi.org/10.1016/bs.aiep.2022.03.003.

Gilgenbach, Colin, Xi Chen, and James M LeBeau. 2024. “A Methodology for Robust Multislice Ptychography.” Microscopy and Microanalysis 30 (4): 703–11. https://doi.org/10.1093/mam/ozae055.

Gladyshev, Anton, Benedikt Haas, Thomas C. Pekin, Tara M. Boland, Marcel Schloz, Peter Rez, and Christoph T. Koch. 2023. “Electron Ptychography Reveals Correlated Lattice Vibrations at Atomic Resolution.” arXiv. https://doi.org/10.48550/ARXIV.2309.12017.

Hawkes, P. W. 1982. “Is the STEM a Ptychograph?” Ultramicroscopy 9 (1): 27–30. https://doi.org/10.1016/0304-3991(82)90225-X.

Hofer, Christoph, Jacob Madsen, Toma Susi, and Timothy J Pennycook. 2025. “Detecting Charge Transfer at Defects in 2D Materials with Electron Ptychography.” Journal of Microscopy.

Hoppe, W. 1969. “Beugung Im Inhomogenen Primärstrahlwellenfeld. I. Prinzip Einer Phasenmessung von Elektronenbeungungsinterferenzen.” Acta Crystallographica Section A 25 (4): 495–501. https://doi.org/10.1107/S0567739469001045.

Hoppe, Walter. 1983. “Electron Diffraction with the Transmission Electron Microscope as a Phase-Determining Diffractometer—from Spatial Frequency Filtering to the Three-Dimensional Structure Analysis of Ribosomes.” Angewandte Chemie International Edition in English 22 (6): 456–85. https://doi.org/10.1002/anie.198304561.

Karapetyan, Shake, Steven E. Zeltmann, Glen Wilk, Ta-Kun Chen, Vincent D. -H. Hou, and David A. Muller. 2025. “3D Atomic-Scale Metrology of Strain Relaxation and Roughness in Gate-All-Around (GAA) Transistors via Electron Ptychography.” arXiv. https://doi.org/10.48550/ARXIV.2507.07265.

Li, Guanxing, Ming Xu, Wen-Qi Tang, Ying Liu, Cailing Chen, Daliang Zhang, Lingmei Liu, et al. 2025. “Atomically Resolved Imaging of Radiation-Sensitive Metal-Organic Frameworks via Electron Ptychography.” Nature Communications 16 (1): 914. https://doi.org/10.1038/s41467-025-56215-z.

Li, Pengcheng, Chenglin Pua, Zehao Dong, Zhengxiong Su, Tao Liu, Chao Cai, Huahai Shen, Lin Gu, and Zhen Chen. 2025. “Atomic-Scale Heterogeneity of Hydrogen in Metal Hydrides Revealed by Electron Ptychography,” no. arXiv:2507.18906 (July). https://doi.org/10.48550/arXiv.2507.18906.

Li, Zhongbo, Harald Rose, Jacob Madsen, Johannes Biskupek, Toma Susi, and Ute Kaiser. 2022. “Computationally Efficient Handling of Partially Coherent Electron Sources in (s)TEM Image Simulations via Matrix Diagonalization.” Microscopy and Microanalysis, September, 1–9. https://doi.org/10.1017/S1431927622012387.

Nellist, P. D., B. C. McCallum, and J. M. Rodenburg. 1995. “Resolution Beyond the ‘Information Limit’ in Transmission Electron Microscopy.” Nature. https://doi.org/10.1038/374630a0.

Pei, Xudong, Liqi Zhou, Chen Huang, Mark Boyce, Judy S. Kim, Emanuela Liberti, Yiming Hu, et al. 2023. “Cryogenic Electron Ptychographic Single Particle Analysis with Wide Bandwidth Information Transfer.” Nature Communications 14 (11): 3027. https://doi.org/10.1038/s41467-023-38268-0.

Pelz, Philipp M., Sinéad M. Griffin, Scott Stonemeyer, Derek Popple, Hannah DeVyldere, Peter Ercius, Alex Zettl, Mary C. Scott, and Colin Ophus. 2023. “Solving Complex Nanostructures with Ptychographic Atomic Electron Tomography.” Nature Communications 14 (11): 7906. https://doi.org/10.1038/s41467-023-43634-z.

Pennycook, Timothy J., Andrew R. Lupini, Hao Yang, Matthew F. Murfitt, Lewys Jones, and Peter D. Nellist. 2015. “Efficient Phase Contrast Imaging in STEM Using a Pixelated Detector. Part 1: Experimental Demonstration at Atomic Resolution.” Ultramicroscopy, Special issue: 80th birthday of harald rose; PICO 2015 – third conference on frontiers of aberration corrected electron microscopy, 151 (April): 160–67. https://doi.org/10.1016/j.ultramic.2014.09.013.

Romanov, Andrey, Min Gee Cho, Mary Cooper Scott, and Philipp Pelz. 2024. “Multi-Slice Electron Ptychographic Tomography for Three-Dimensional Phase-Contrast Microscopy Beyond the Depth of Focus Limits.” Journal of Physics: Materials 8 (1): 015005. https://doi.org/10.1088/2515-7639/ad9ad2.

Sha, Haozhi, Jizhe Cui, and Rong Yu. 2022. “Deep Sub-Angstrom Resolution Imaging by Electron Ptychography with Misorientation Correction.” Science Advances 8 (19): eabn2275. https://doi.org/10.1126/sciadv.abn2275.

Skoupy, Radim, Elisabeth Müller, Timothy J. Pennycook, Manuel Guizar-Sicairos, Emiliana Fabbri, and Emiliya Poghosyan. 2025. “Ptychoscopy: A User Friendly Experimental Design Tool for Ptychography.” Scientific Reports 15 (1): 24959. https://doi.org/10.1038/s41598-025-09871-6.

Thibault, Pierre, and Andreas Menzel. 2013. “Reconstructing State Mixtures from Diffraction Measurements.” Nature 494 (7435): 68–71. https://doi.org/10.1038/nature11806.

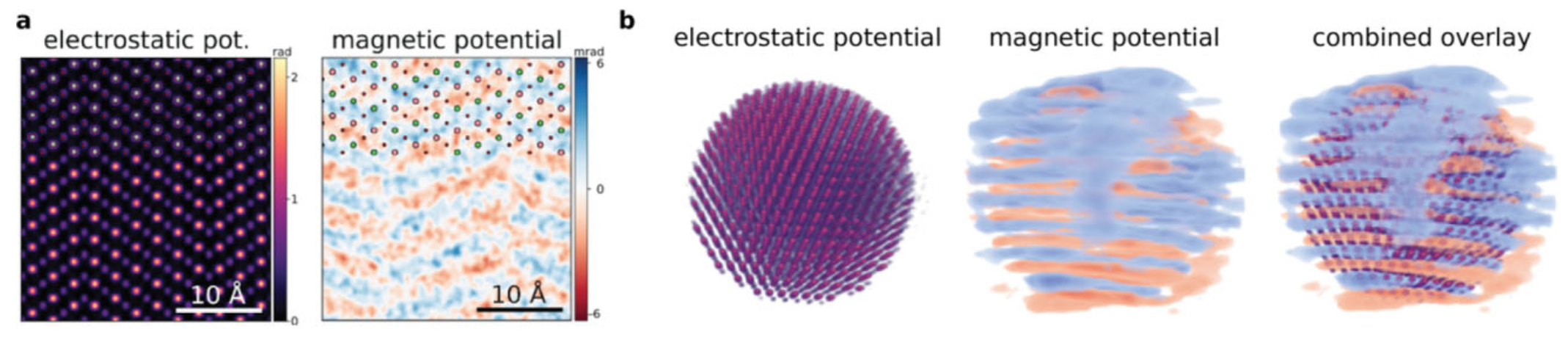
Yalisove, Reed, Georgios Varnavides, and Mary C Scott. 2025. “Toward Imaging of Antiferromagnetic Ordering at the Atomic Scale.” Microscopy and Microanalysis 31 (Supplement_1). https://doi.org/10.1093/mam/ozaf048.1124.

Yang, Hao, Peter Ercius, Peter D. Nellist, and Colin Ophus. 2016. “Enhanced Phase Contrast Transfer Using Ptychography Combined with a Pre-Specimen Phase Plate in a Scanning Transmission Electron Microscope.” Ultramicroscopy 171 (December): 117–25. https://doi.org/10/f9fwhk.

Yang, Wenfeng, Haozhi Sha, Jizhe Cui, Liangze Mao, and Rong Yu. 2024. “Local-Orbital Ptychography for Ultrahigh-Resolution Imaging.” Nature Nanotechnology, January, 1–6. https://doi.org/10.1038/s41565-023-01595-w.

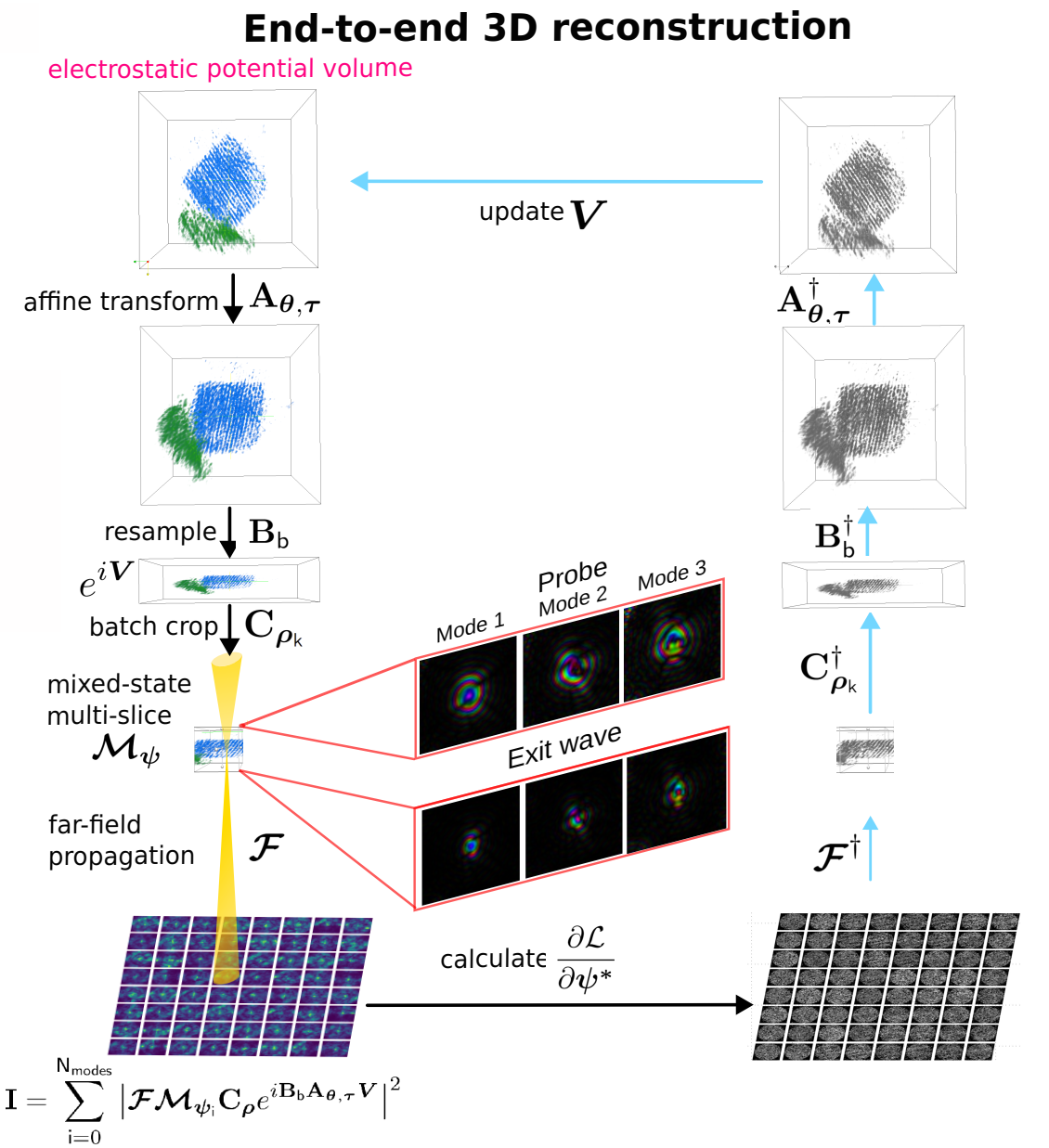
You, Shengbo, Andrey Romanov, and Philipp M Pelz. 2024. “Near-Isotropic Sub-Ångstrom 3d Resolution Phase Contrast Imaging Achieved by End-to-End Ptychographic Electron Tomography.” Physica Scripta 100 (1): 015404. https://doi.org/10.1088/1402-4896/ad9a1a.

Zhang, Hui, Guanxing Li, Jiaxing Zhang, Daliang Zhang, Zhen Chen, Xiaona Liu, Peng Guo, et al. 2023. “Three-Dimensional Inhomogeneity of Zeolite Structure and Composition Revealed by Electron Ptychography.” Science 380 (6645): 633–38. https://doi.org/10.1126/science.adg3183.

Tutorial Links

• 01 Weak Phase
• 02 Single Slice
• 03 Multi Slice

This talk