Data Science for Electron Microscopy
Lecture 3: Convolutional Neural Networks

Philipp Pelz

FAU Erlangen-Nürnberg

FAU Logo IMN Logo CENEM Logo Elettra Logo

From Fully Connected Layers to Convolutions

Key Points

  • MLPs impractical for high-dimensional perceptual data
  • One-megapixel image → \(10^9\) parameters with 1000 hidden units
  • CNNs exploit rich image structure

Three Key CNN Design Principles

Core Principles

  1. Translation Invariance: Network responds similarly to patterns regardless of location
  2. Locality: Early layers focus on local regions
  3. Hierarchy: Deeper layers capture longer-range features

Invariance in Object Detection

Key Concept

  • Recognition should not depend on precise object location
  • Illustrated by “Where’s Waldo” game
  • Waldo’s appearance independent of location
  • Sweep image with detector for likelihood scores

An image of the “Where’s Waldo” game.

CNN Design Desiderata

  1. Translation Invariance
    • Early layers respond similarly to same patch
    • Regardless of location in image
  2. Locality
    • Early layers focus on local regions
    • Aggregate local representations later
  1. Hierarchy
    • Deeper layers capture longer-range features
    • Similar to higher-level vision in nature

Constraining the MLP

Mathematical Formulation

  • Input images \(\mathbf{X}\) and hidden representations \(\mathbf{H}\) as matrices
  • Fourth-order weight tensors \(\mathsf{W}\)
  • With biases \(\mathbf{U}\):

\[\begin{aligned} \left[\mathbf{H}\right]_{i, j} &= [\mathbf{U}]_{i, j} + \sum_k \sum_l[\mathsf{W}]_{i, j, k, l} [\mathbf{X}]_{k, l}\\ &= [\mathbf{U}]_{i, j} + \sum_a \sum_b [\mathsf{V}]_{i, j, a, b} [\mathbf{X}]_{i+a, j+b}.\end{aligned}\]

Translation Invariance

Key Insight

  • Shift in input \(\mathbf{X}\) → shift in hidden representation \(\mathbf{H}\)
  • \(\mathsf{V}\) and \(\mathbf{U}\) independent of \((i, j)\)
  • Simplified definition:

\[[\mathbf{H}]_{i, j} = u + \sum_a\sum_b [\mathbf{V}]_{a, b} [\mathbf{X}]_{i+a, j+b}.\]

  • This is a convolution!

Locality

Implementation

  • Only look near location \((i, j)\)
  • Set \([\mathbf{V}]_{a, b} = 0\) outside range \(|a|> \Delta\) or \(|b| > \Delta\)
  • Rewritten as:

\[[\mathbf{H}]_{i, j} = u + \sum_{a = -\Delta}^{\Delta} \sum_{b = -\Delta}^{\Delta} [\mathbf{V}]_{a, b} [\mathbf{X}]_{i+a, j+b}.\]

  • Reduces parameters from \(4 \cdot 10^6\) to \(4 \Delta^2\)

Convolutions in Mathematics

Definition

  • Convolution between functions \(f, g: \mathbb{R}^d \to \mathbb{R}\):

\[(f * g)(\mathbf{x}) = \int f(\mathbf{z}) g(\mathbf{x}-\mathbf{z}) d\mathbf{z}.\]

  • For discrete objects (2D tensors):

\[(f * g)(i, j) = \sum_a\sum_b f(a, b) g(i-a, j-b).\]

Channels in CNNs

Key Concepts

  • Images: 3 channels (RGB)
  • Third-order tensors: height × width × channel
  • Convolutional filter adapts: \([\mathsf{V}]_{a,b,c}\)
  • Hidden representations: third-order tensors \(\mathsf{H}\)
  • Feature maps: spatialized learned features

Detect Waldo.

Multi-Channel Convolution

Complete Formulation

  • Input channels: \(c_i\)
  • Output channels: \(c_o\)
  • Kernel shape: \(c_o\times c_i\times k_h\times k_w\)
  • Complete convolution:

\([\mathsf{H}]_{i,j,d} = \sum_{a = -\Delta}^{\Delta} \sum_{b = -\Delta}^{\Delta} \sum_c [\mathsf{V}]_{a, b, c, d} [\mathsf{X}]_{i+a, j+b, c},\)

where \(d\) indexes output channels

Summary and Discussion

Key Points

  • CNNs derived from first principles
  • Translation invariance: treat all patches similarly
  • Locality: use small neighborhoods
  • Channels: restore complexity lost to restrictions
  • Hyperspectral images: tens to hundreds of channels :::

Convolutions for Images

Code 
import d2l
import torch
from torch import nn

The Cross-Correlation Operation

Key Points

  • Convolutional layers actually perform cross-correlation
  • Input tensor and kernel tensor combined
  • Window slides across input tensor
  • Elementwise multiplication and summation

Two-dimensional cross-correlation operation

Cross-Correlation Implementation

def corr2d(X, K):  #@save
    """Compute 2D cross-correlation."""
    h, w = K.shape
    Y = d2l.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = d2l.reduce_sum((X[i: i + h, j: j + w] * K))
    return Y

Cross-Correlation Example

# Create a 256x256 sparse image with a few 1s
X = torch.zeros((64, 64))
X[11, 23] = 1.0
X[23, 23] = 1.0
X[56, 48] = 1.0
X[19, 54] = 1.0

# Create a 3x3 cross-shaped kernel
K = torch.tensor([[0.0, 1.0, 0.0],
                 [1.0, 1.0, 1.0],
                 [0.0, 1.0, 0.0]])

# Apply the correlation
Y = corr2d(X, K)

import matplotlib.pyplot as plt

fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))

# Plot input image X
ax1.imshow(X, cmap='gray')
ax1.set_title('Input Image (X)')
ax1.axis('on')

# Plot kernel K
ax2.imshow(K, cmap='gray')
ax2.set_title('Kernel (K)')
ax2.axis('on')

# Plot output Y
ax3.imshow(Y, cmap='gray')
ax3.set_title('Output (Y)')
ax3.axis('on')

plt.tight_layout()
plt.show()

Convolutional Layers

Implementation

  • Cross-correlate input and kernel
  • Add scalar bias
  • Initialize kernels randomly
  • Parameters: kernel and scalar bias
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

Edge Detection Example

Application

  • Detect object edges in images
  • Find pixel change locations
  • Use special kernel for edge detection
X = d2l.ones((6, 8))
X[:, 2:6] = 0
X
K = d2l.tensor([[1.0, -1.0]])
Y = corr2d(X, K)
Y

Learning a Kernel

Training Process

  • Learn kernel from input-output pairs
  • Use squared error loss
  • Update kernel via gradient descent
conv2d = nn.LazyConv2d(1, kernel_size=(1, 2), bias=False)
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i + 1}, loss {l.sum():.3f}')

Cross-Correlation vs Convolution

Key Differences

  • Strict convolution: flip kernel horizontally and vertically
  • Cross-correlation: use original kernel
  • Outputs remain same due to learned kernels
  • Term “convolution” used for both operations

Feature Maps and Receptive Fields

Concepts

  • Feature map: learned spatial representations
  • Receptive field: elements affecting calculation
  • Can be larger than input size
  • Deeper networks for larger receptive fields

Figure from Field (1987): Coding with six different channels

Summary

Key Points

  • Core computation: cross-correlation
  • Multiple channels: matrix-matrix operations
  • Highly local computation
  • Hardware optimization opportunities
  • Learnable filters replace feature engineering

Exercises

Practice Problems

  1. Diagonal edges and kernel effects
  2. Manual kernel design
  3. Gradient computation errors
  4. Cross-correlation as matrix multiplication
  5. Fast convolution algorithms
  6. Block-diagonal matrix multiplication

Padding and Stride

Motivation

  • Control output size
  • Prevent information loss
  • Handle large kernels
  • Reduce spatial resolution
import torch
from torch import nn

Padding

Key Concepts

  • Add extra pixels around boundary
  • Typically zero padding
  • Preserve spatial dimensions
  • Common with odd kernel sizes

Pixel utilization for different convolution sizes

Padding Implementation

def comp_conv2d(conv2d, X):
    X = X.reshape((1, 1) + X.shape)
    Y = conv2d(X)
    return Y.reshape(Y.shape[2:])

conv2d = nn.LazyConv2d(1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape

Stride

Key Points

  • Move window more than one element
  • Skip intermediate locations
  • Useful for large kernels
  • Control output resolution

Cross-correlation with strides of 3 and 2

Stride Implementation

conv2d = nn.LazyConv2d(1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape

conv2d = nn.LazyConv2d(1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape

Summary and Discussion

Key Points

  • Padding: control output dimensions
  • Stride: reduce resolution
  • Zero padding: computational benefits
  • Position information encoding
  • Alternative padding methods

Multiple Input and Output Channels

Key Concepts

  • RGB images: 3 channels
  • Input shape: \(3\times h\times w\)
  • Channel dimension: size 3
  • Multiple input/output channels

Multiple Input Channels

Implementation

  • Kernel matches input channels
  • Shape: \(c_i\times k_h\times k_w\)
  • Cross-correlation per channel
  • Sum results
def corr2d_multi_in(X, K):
    return sum(d2l.corr2d(x, k) for x, k in zip(X, K))

X = d2l.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = d2l.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)

Multiple Output Channels

Implementation

  • Kernel tensor for each output channel
  • Shape: \(c_o\times c_i\times k_h\times k_w\)
  • Concatenate on output channel dimension
def corr2d_multi_in_out(X, K):
    return d2l.stack([corr2d_multi_in(X, k) for k in K], 0)

K = d2l.stack((K, K + 1, K + 2), 0)
K.shape

corr2d_multi_in_out(X, K)

\(1\times 1\) Convolutional Layer

Key Points

  • No spatial correlation
  • Channel dimension computation
  • Linear combination at each position
  • Fully connected layer per pixel

\(1\times 1\) convolution with 3 input and 2 output channels

\(1\times 1\) Convolution Implementation

def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = d2l.reshape(X, (c_i, h * w))
    K = d2l.reshape(K, (c_o, c_i))
    Y = d2l.matmul(K, X)
    return d2l.reshape(Y, (c_o, h, w))

X = d2l.normal(0, 1, (3, 3, 3))
K = d2l.normal(0, 1, (2, 3, 1, 1))
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
# assert float(d2l.reduce_sum(d2l.abs(Y1 - Y2))) < 1e-6

Discussion

Key Points

  • Channels combine MLP and CNN benefits
  • Trade-off: parameter reduction vs. model expressiveness
  • Computational cost: \(\mathcal{O}(h \cdot w \cdot k^2 \cdot c_i \cdot c_o)\)
  • Example: 256×256 image, 5×5 kernel, 128 channels → 53B operations

Pooling

Motivation

  • Global questions about images
  • Gradual information aggregation
  • Translation invariance
  • Spatial downsampling

Maximum and Average Pooling

Key Concepts

  • Fixed-shape window
  • No parameters
  • Deterministic operations
  • Maximum or average value

Max-pooling with \(2\times 2\) window

Pooling Implementation

def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = d2l.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

X = d2l.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))
pool2d(X, (2, 2), 'avg')

Padding and Stride in Pooling

Implementation

  • Adjust output shape
  • Default: matching window and stride
  • Manual specification possible
  • Rectangular windows supported
X = d2l.reshape(d2l.arange(16, dtype=d2l.float32), (1, 1, 4, 4))
X

pool2d = nn.MaxPool2d(3)
pool2d(X)

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)

Multiple Channels in Pooling

Key Points

  • Pool each channel separately
  • Maintain channel count
  • Independent operations
X = d2l.concat((X, X + 1), 1)
X

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

Summary

Key Points

  • Simple aggregation operation
  • Standard convolution semantics
  • Channel independence
  • Max-pooling preferred
  • \(2 \times 2\) window common
  • Alternative pooling methods

Summary

Key Points

  • Evolution from MLPs to CNNs
  • LeNet-5 remains relevant
  • Similar to modern architectures
  • Implementation ease
  • Democratized deep learning

Introduction to Modern CNNs

Key Points

  • Tour of modern CNN architectures
  • Simple concept: stack layers together
  • Performance varies with architecture and hyperparameters
  • Based on intuition, math insights, and experimentation
  • Batch normalization and residual connections are key innovations

Historical Architectures

Key Milestones

  • AlexNet (2012): First large-scale network to beat conventional methods
  • VGG (2014): Introduced repeating block patterns
  • NiN (2013): Convolved neural networks patch-wise
  • DenseNet (2017): Generalized residual architecture

Pre-CNN Classical Pipeline

Traditional Approach

  1. Obtain dataset (e.g., Apple QuickTake 100, 1994)
  2. Preprocess with hand-crafted features
  3. Use standard feature extractors (SIFT, SURF)
  4. Feed to classifier (linear model/kernel method)
Code 
import d2l
import torch
from torch import nn
Figure 1

Representation Learning Evolution

  • Pre-2012: Mechanical feature calculation
  • Common features:
    • SIFT
    • SURF
    • HOG
    • Bags of visual words

Modern Approach

  • Features learned automatically
  • Hierarchical composition
  • Multiple jointly learned layers
  • Learnable parameters

Feature Learning in CNNs

Layer Progression

  • Lowest layers: edges, colors, textures
  • Analogous to animal visual system
  • Automatic feature design
  • Modern CNNs revolutionized approach

Image filters learned by AlexNet’s first layer

VGG: Networks Using Blocks

Key Innovation

  • Evolution from individual neurons to layers to blocks
  • Similar to VLSI design progression
  • Pioneered repeated block structures
  • Foundation for modern models

VGG Block Structure

Basic Building Block

  • Convolutional layer with padding
  • Nonlinearity (ReLU)
  • Pooling layer

Key Innovation

  • Multiple 3×3 convolutions between pooling
  • Two 3×3 = one 5×5 receptive field
  • Three 3×3 ≈ one 7×7
  • Deep and narrow networks perform better
def vgg_block(num_convs, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.LazyConv2d(out_channels, 
                                  kernel_size=3, 
                                  padding=1))
        layers.append(nn.ReLU())
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

VGG Network Architecture

Two Main Parts

  1. Convolutional and pooling layers
  2. Fully connected layers (like AlexNet)

Key Difference

  • Convolutional layers grouped in blocks
  • Nonlinear transformations
  • Resolution reduction steps

From AlexNet to VGG

VGG Implementation

class VGG(d2l.Classifier):
    def __init__(self, arch, lr=0.1, num_classes=10):
        super().__init__()
        self.save_hyperparameters()
        conv_blks = []
        for (num_convs, out_channels) in arch:
            conv_blks.append(vgg_block(num_convs, out_channels))
        self.net = nn.Sequential(
            *conv_blks, nn.Flatten(),
            nn.LazyLinear(4096), nn.ReLU(), nn.Dropout(0.5),
            nn.LazyLinear(4096), nn.ReLU(), nn.Dropout(0.5),
            nn.LazyLinear(num_classes))
        self.net.apply(d2l.init_cnn)

VGG Layer Summary

VGG(arch=((1, 64), (1, 128), (2, 256), 
          (2, 512), (2, 512))).layer_summary(
    (1, 1, 224, 224))

VGG Training

Important Notes

  • VGG-11 more demanding than AlexNet
  • Smaller number of channels for Fashion-MNIST
  • Similar training process to AlexNet
  • Close match between validation and training loss
model = VGG(arch=((1, 16), (1, 32), (2, 64), 
                  (2, 128), (2, 128)), lr=0.01)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128, resize=(224, 224))
model.apply_init([next(iter(data.get_dataloader(True)))[0]], 
                d2l.init_cnn)
# trainer.fit(model, data)

VGG Summary

Key Contributions

  • First truly modern CNN
  • Introduced block-based design
  • Preference for deep, narrow networks
  • Family of similarly parametrized models

Network in Network (NiN)

Design Challenges

  • Fully connected layers consume huge memory
  • Adding nonlinearity can destroy spatial structure

NiN Solution

  • Use 1×1 convolutions for local nonlinearities
  • Global average pooling instead of fully connected layers

NiN Architecture

Key Differences from VGG

  • Applies fully connected layer at each pixel
  • Uses 1×1 convolutions after initial convolution
  • Eliminates need for large fully connected layers

Comparing VGG and NiN architectures

NiN Block Implementation

def nin_block(out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.LazyConv2d(out_channels, kernel_size, strides, padding), 
        nn.ReLU(),
        nn.LazyConv2d(out_channels, kernel_size=1), nn.ReLU(),
        nn.LazyConv2d(out_channels, kernel_size=1), nn.ReLU())

NiN Model

Architecture Details

  • Initial convolution sizes like AlexNet
  • NiN block with output channels = number of classes
  • Global average pooling layer
  • Significantly fewer parameters
class NiN(d2l.Classifier):
    def __init__(self, lr=0.1, num_classes=10):
        super().__init__()
        self.save_hyperparameters()
        self.net = nn.Sequential(
            nin_block(96, kernel_size=11, strides=4, padding=0),
            nn.MaxPool2d(3, stride=2),
            nin_block(256, kernel_size=5, strides=1, padding=2),
            nn.MaxPool2d(3, stride=2),
            nin_block(384, kernel_size=3, strides=1, padding=1),
            nn.MaxPool2d(3, stride=2),
            nn.Dropout(0.5),
            nin_block(num_classes, kernel_size=3, strides=1, padding=1),
            nn.AdaptiveAvgPool2d((1, 1)),
            nn.Flatten())
        self.net.apply(d2l.init_cnn)

NiN Layer Summary

NiN().layer_summary((1, 1, 224, 224))

NiN Training

model = NiN(lr=0.05)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128, resize=(224, 224))
model.apply_init([next(iter(data.get_dataloader(True)))[0]], 
                d2l.init_cnn)
# trainer.fit(model, data)

NiN Summary

Key Advantages

  • Dramatically fewer parameters
  • No giant fully connected layers
  • Global average pooling
  • Simple averaging operation
  • Translation invariance
  • Nonlinearity across channels

Batch Normalization

Benefits

  • Accelerates network convergence
  • Enables training of very deep networks
  • Provides inherent regularization
  • Makes optimization landscape smoother

Training Deep Networks

Data Preprocessing

  • Standardize input features
  • Zero mean and unit variance
  • Constrain function complexity
  • Put parameters at similar scale

Batch Normalization Layers

Fully Connected Layers

  • After affine transformation
  • Before nonlinear activation
  • Normalize across minibatch

Convolutional Layers

  • After convolution
  • Before nonlinear activation
  • Per-channel basis
  • Across all locations
def conv_block(num_channels):
    return nn.Sequential(
        nn.LazyBatchNorm2d(), nn.ReLU(),
        nn.LazyConv2d(num_channels, kernel_size=3, padding=1))

Layer Normalization

Key Features

  • Applied to one observation at a time
  • Offset and scaling factor are scalars
  • Prevents divergence
  • Scale independent
  • Independent of minibatch size

Batch Normalization During Prediction

Important Notes

  • Different behavior in training vs prediction
  • Use entire dataset for statistics
  • Fixed statistics at prediction time
  • Similar to dropout behavior

DenseNet

Key Features

  • Logical extension of ResNet
  • Each layer connects to all preceding layers
  • Concatenation instead of addition
  • Preserves and reuses features

DenseNet Architecture

Key Components

  • Dense blocks
  • Transition layers
  • Concatenation operation
  • Feature reuse

DenseNet connections

DenseNet Implementation

class DenseBlock(nn.Module):
    def __init__(self, num_convs, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            X = torch.cat((X, Y), dim=1)
        return X

Transition Layers

def transition_block(num_channels):
    return nn.Sequential(
        nn.LazyBatchNorm2d(), nn.ReLU(),
        nn.LazyConv2d(num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))

DenseNet Model

class DenseNet(d2l.Classifier):
    def b1(self):
        return nn.Sequential(
            nn.LazyConv2d(64, kernel_size=7, stride=2, padding=3),
            nn.LazyBatchNorm2d(), nn.ReLU(),
            nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

    def __init__(self, num_channels=64, growth_rate=32, 
                 arch=(4, 4, 4, 4), lr=0.1, num_classes=10):
        super(DenseNet, self).__init__()
        self.save_hyperparameters()
        self.net = nn.Sequential(self.b1())
        for i, num_convs in enumerate(arch):
            self.net.add_module(f'dense_blk{i+1}', 
                              DenseBlock(num_convs, growth_rate))
            num_channels += num_convs * growth_rate
            if i != len(arch) - 1:
                num_channels //= 2
                self.net.add_module(f'tran_blk{i+1}', 
                                  transition_block(num_channels))
        self.net.add_module('last', nn.Sequential(
            nn.LazyBatchNorm2d(), nn.ReLU(),
            nn.AdaptiveAvgPool2d((1, 1)), nn.Flatten(),
            nn.LazyLinear(num_classes)))
        self.net.apply(d2l.init_cnn)

DenseNet Training

model = DenseNet(lr=0.01)
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128, resize=(96, 96))
# trainer.fit(model, data)

U-Net Architecture

Key Features

  • Originally for biomedical image segmentation
  • Symmetric encoder-decoder structure
  • Skip connections
  • Works with limited training data
  • Preserves spatial information

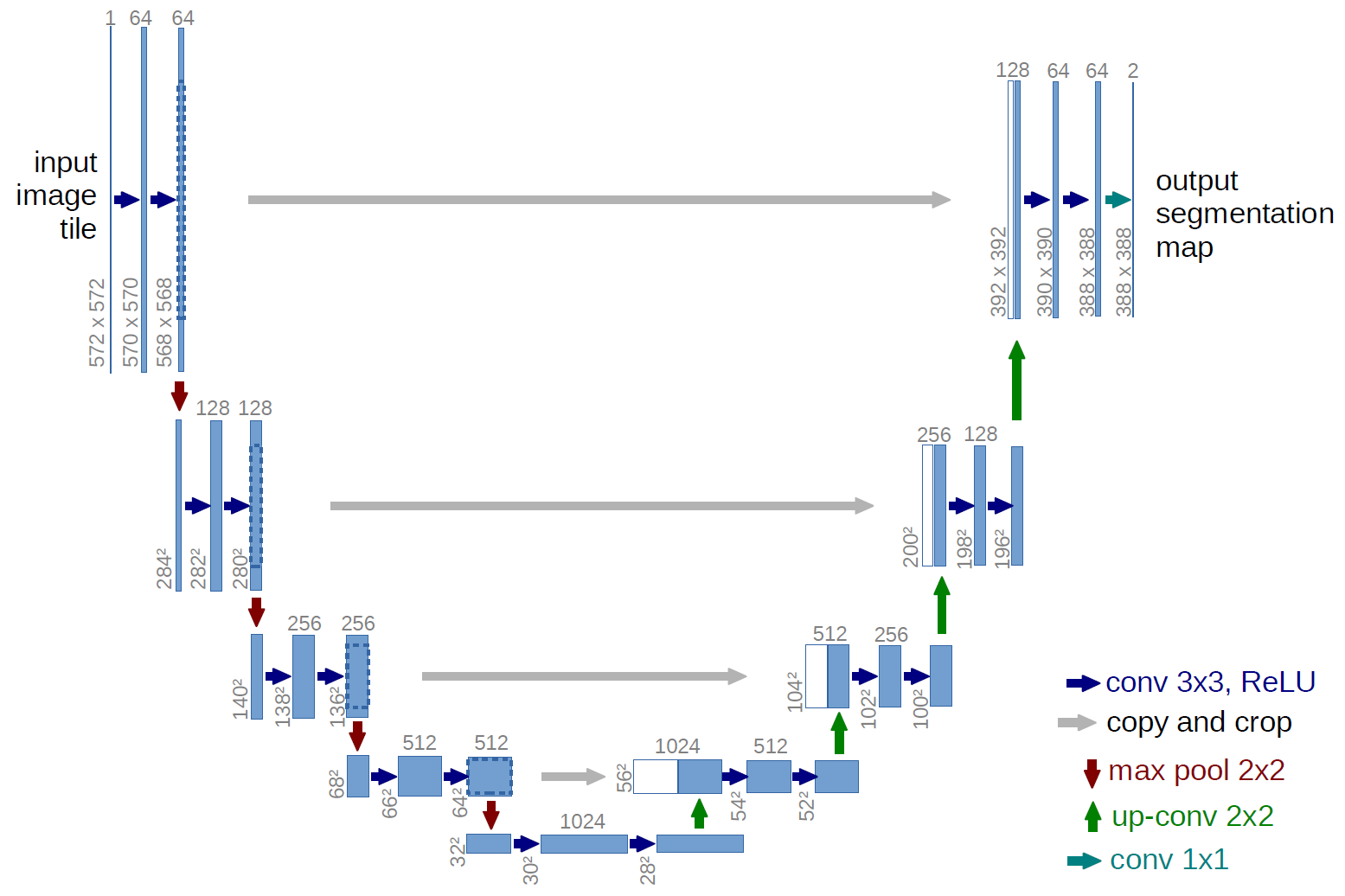
U-Net architecture

U-Net Components

Contracting Path

  • Convolutional layers
  • Max pooling
  • Doubles feature channels
  • Reduces spatial dimensions

Expansive Path

  • Upsampling
  • Feature concatenation
  • Successive convolutions
  • Recovers resolution

U-Net Implementation

class UNetBlock(nn.Module):
    def __init__(self, in_channels, out_channels):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, 3, padding=1)
        self.conv2 = nn.Conv2d(out_channels, out_channels, 3, padding=1)
        self.relu = nn.ReLU()
    
    def forward(self, x):
        x = self.relu(self.conv1(x))
        x = self.relu(self.conv2(x))
        return x

U-Net Applications

Use Cases

  • Medical image segmentation
  • Object detection
  • Industrial defect detection
  • General segmentation tasks

Advantages

  • Works with limited data
  • Precise localization
  • End-to-end training
  • Fast inference

References